Пример. Определение объема траншеи

По форулам (1.34) получаем
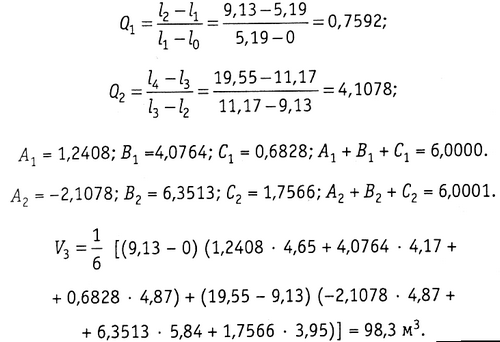
Для оценки точности полученного по формуле паробол результата используют приближенную формулу
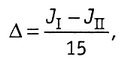
где JI, JII — значения интеграла, полученного при шаге интегрирования q и 2q соответственно. В рассматриваемом примере JI = V3 = 98,3 м3, при удвоенном шаге интегрирования имеем

что составляет 0,5% от величины V. Поэтому значение V3 полученное по формуле парабол, можно считать достаточно точным.
Расхождение между значениями V1-V3 = -14,2
м3, что составляет 15,65% от 0,5 (V1+
V3); разность V2 - V3 = -5,7
м3, что составляет 6,0% от 0,5 (V2 +
V3).
Следовательно, более тичное значение
V3, определяемое по формуле парабол (с ошибкой около 0,5%),
можно получить при тех же исходных данных, что и по формуле трапеций. Поэтому
для более точного определения объема траншеи целесообразно использовать формулу
(1.34), вычисляя площади сечений траншеи в наиболее характерных точках.
Рассмотренные методы можно использовать для вычисления объемов выемок при строительстве каналов, автомобильных и железных дорог. При сложной конструкции земляного полотна и изменчивости рельефа местности для определения площади сечения используют графическое построение сечения - эффективно для этой цели используют компьютеры.
Для определения объема грунта в дамбе можно использовать формулы, применяемые для определения объема траншеи.

